How do you teach Gauss' Law?
It's a serious question which depends largely on the audience. Students who are learning this in an algebra-based physics class are often learning Gauss' Law as a "gee-whiz" phenomena rather than as a serious computational tool, and as such, they may ultimately memorize a handful of charge distributions for which it works (if that!). Students in a calculus-based class will often start with flux and then make it to the usual Maxwell equation:
Next they learn to apply this equation to a bunch of geometric situations. However, for many students, this smacks of black magick and arcane knowledge. How, for example, do we know the exact direction of the electric field? How do we choose a Gaussian surface? Although one can discuss surface normals and trying to ensure that the Gaussian surface normals are, in fact, parallel to the electric field, this sometimes seems circular to students. The result is memorization of certain charge configurations.
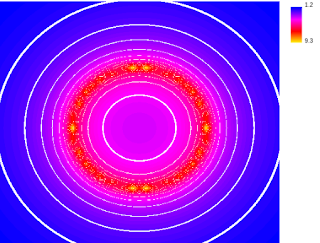
As I've thought about this over the years, it has occurred to me that starting from equipotential surfaces might be the way to go. Consider a 2D ring of charge. The following image shows what this charge's scalar potential field will look like. The charge has, of course been broken into a number of discreet charges, so it doesn't look like a perfect ring of charge. But it's close, really close.
The units of this graph are in volts. Equipotential curves are drawn in white around the distribution. The equipotential curves for such symmetrical distributions indicate where the Gaussian surface should go. If your students are used to visualizing equipotentials, then they also have a sense of which Gaussian surface to pick. And so long as the charge distribution is fairly symmetrical, the electric field on that surface will be constant. (I won't get into trying to use Gauss' Law with dipoles or the like, since then the electric field has azimuthal components as well, and Coulomb's Law is probably easier to apply.)
Code to generate this sort of charge distribution (in the interest of visualizing equipotentials) using JSvg2 follows below. I'll discuss the generation of equipotential graphs in another post.
First the code to calculate the Coulomb potential at a field point given the position and charge of the source charge, and the position of the field point.
function calcPotential(qS, xS, yS, xF, yF) {
// qS - source charge
// xS, yS - source x,y positions
// xF, yF - field x,y positions
var k=8.99e9; // N*m^2/C^2
var thresh = 20; // Max abs value of voltage to display
var dx = xF - xS; // Difference in x and y between source and field pts
var dy = yF - yS;
var r = Math.sqrt( dx*dx + dy*dy ); // Pythagorean distance
// between source and field points
var V = k*qS/r; // Potential in units of volts
if (V > thresh) V = thresh; // For display purposes
if (V < -thresh) V = -thresh;
return V;
}
Next, define some preliminaries.
In this diagram, the boundaries of the scalar potential field are given by (xo,yo) on the upper left, and (x1,y1) on the lower right. The coordinate system for computer graphics is left handed, unfortunately. We define a total charge, Q, which will be spread out into N discreet point charges along a circle of radius R1. The angular increment between point charges is dphi. We will store our scalar potential field in the array V, and our charge distribution from which it is generated in the array chargeArr.
// Here V is a 1D array
var V = []; // A global array in which to store my potential field
var d2r = Math.PI/180; // Degree to radian conversion
// Define the boundaries of our potential field
var xo = -10.5; // m
var yo = -10.5; // m
var x1 = +10.5; // m
var y1 = +10.5; // m
var Q = 1.0e-8; // total charge on the bar
var N = 90; // There will be N charges!
var dphi = 360/N; // Angular increment to go around the circle
var R1 = 5.0; // m - Radius of circle
var dq = Q/N; // the amount of charge - on each charge in circle
var chargeArr = []; // new array to store charges
Next, we fill the array by starting on the x-axis at a distance R1 from the origin, and then proceeding counter-clockwise around the circle. As we change the phi position, we recalculate the x and y positions of the point charges using trigonometry. Each charge in chargeArr is itself an array of three elements, [q,x,y], that is, charge, x-position, and y-position.
var ya = 0; // Initial y and x position of charges in array
var xa = R1;
for (var i=0; i< N; i++) {
chargeArr[i] = [dq,xa,ya];
// Update angle around the circle
var phi = (i+1)*dphi;
var phiR = phi*d2r; // Then convert it to radians
xa = R1*Math.cos(phiR); // New x and y positions
ya = R1*Math.sin(phiR);
}
Next, we actually calculate the potential at each point in the grid. We start at xo, yo. Then we step through all the y-values of the grid (changed by adding dy1 to the prior y-value). Then, we set y back to yo, add dx1 to xo, and then step through y again.
// initialize 2 counters - one for the x direction: i
// - one for the y direction: j
// The purpose of the counters is to index the V array.
var i=0; // Counter along x direction
var dx1 = 0.5; // scalar field sampling is 1/10 of a meter
var dy1 = 0.5; // instead of a meter
// Use embedded loops to change field positions
for (var x=xo; x<=x1; x+=dx1) {
V[i] = []; // Initialize ith value of V array as an embedded 1D array
j=0; // Counter along y direction, initialize to zero prior to
// looping over y.
for (var y=yo; y<=y1; y+=dy1) {
V[i][j] = 0; // Initialization
//console.log("V[i][j] = "+V[i][j]+", x = "+x+", y = "+y)
for (var ii=0; ii< chargeArr.length; ii++) {
var charge = chargeArr[ii]; // The ii-th charge in chargeArr
var qa = charge[0]; // the charge of this charge
var xa = charge[1]; // the x and y positions of this charge
var ya = charge[2];
// Update the potential using superposition
V[i][j] += calcPotential(qa, xa, ya, x, y);
}
j++; // Increment this each time through the y loop
}
i++; // Increment this each time through the x loop
}
Finally, we use some plotting code from JSvg2. Note that everything above this is doable in generic JavaScript. What comes below is not. You need to have the JSvg2 library and its associated functions to work. In any event, the inputs are the colortable of choice, the x and y dimensions of the image, and the number of contours you want drawn. This code takes the input array V and performs a linear interpolation across x and y to estimate in-between values before displaying them.
colortable = 0; // What color do you want the output to be xdim = 500; // How big a grid do you want ydim = 500; // nContours = 15; // How many equipotentials should be drawn // Draw it - only works on http://www.niiler.com/JSvg2/analysis.html field_setupColorMap(V,colortable,xdim,ydim,nContours);
The class had previously worked at creating all kinds of equipotential fields from different charge distributions, so when I projected this image on the whiteboard, they knew what they were looking at. I then had a student come up and draw the electric field lines that corresponded to the equipotentials. He nailed it. They were all perpendicular as should be. (His drawing was somewhat similar to what is below - arrows pointing outwards)
Next, I asked the class how many field lines went through each circle. Answer: the same number. Then I asked if the field was getting stronger or weaker as one moved away. There were several answers. Some students remembered the Coulomb field of a point charge decreasing as one over r-squared. Others said that the field lines were spreading out as one moved further from the charges, and that therefore, the field strength was decreasing. Then I told them to imagine this as a 3D scenario. What shape would the equipotentials be? "Spherical" was the answer. Which way would the field lines be pointing compared to the equipotentials? "Right angles." Next: how did the field strength times the surface area compare from an inner surface to an outer surface. After some discussion, the students arrived at the answer: "it didn't." Outer surfaces had larger surface areas and weaker E fields, while inner surfaces had smaller surface areas and stronger E fields. They balanced out.
It was only at this point that we began to talk about the formalities of Gaussian surfaces, flux, and surface normals. By the end of the class, the students were able to apply Gauss' Law to a solid sphere of charge, and a solid cylinder of charge. And rather than memorizing the shapes of the surfaces, they were able to reason out why the chosen Gaussian surfaces had their shapes, and how conservation of flux was relevant.
This is not the be all and end all of teaching Gauss' Law to 2nd semester calculus-based physics students. I'm sure there are some other good ways to present the material. But it certainly is the best way I've presented it in the nearly 8 years I've been teaching this class.
Cheers!